A Tutorial on Clustering Algorithms

Introduction | K-means | Fuzzy C-means | Hierarchical | Mixture of Gaussians | Links

Hierarchical Clustering Algorithms

How They Work
Given a set of N items to be clustered, and an N*N distance (or similarity) matrix, the basic process of hierarchical clustering (defined by S.C. Johnson in 1967) is this:

1. Start by assigning each item to a cluster, so that if you have N items, you now have N clusters, each containing just one item. Let the distances (similarities) between the clusters the same as the distances (similarities) between the items they contain.
2. Find the closest (most similar) pair of clusters and merge them into a single cluster, so that now you have one cluster less.
3. Compute distances (similarities) between the new cluster and each of the old clusters.
4. Repeat steps 2 and 3 until all items are clustered into a single cluster of size N. (*)

Step 3 can be done in different ways, which is what distinguishes single-linkage from complete-linkage and average-linkage clustering.
In single-linkage clustering (also called the connectedness or minimum method), we consider the distance between one cluster and another cluster to be equal to the shortest distance from any member of one cluster to any member of the other cluster. If the data consist of similarities, we consider the similarity between one cluster and another cluster to be equal to the greatest similarity from any member of one cluster to any member of the other cluster.
In complete-linkage clustering (also called the diameter or maximum method), we consider the distance between one cluster and another cluster to be equal to the greatest distance from any member of one cluster to any member of the other cluster.
In average-linkage clustering, we consider the distance between one cluster and another cluster to be equal to the average distance from any member of one cluster to any member of the other cluster.
A variation on average-link clustering is the UCLUS method of R. D'Andrade (1978) which uses the median distance, which is much more outlier-proof than the average distance.

This kind of hierarchical clustering is called agglomerative because it merges clusters iteratively. There is also a divisive hierarchical clustering which does the reverse by starting with all objects in one cluster and subdividing them into smaller pieces. Divisive methods are not generally available, and rarely have been applied.

(*) Of course there is no point in having all the N items grouped in a single cluster but, once you have got the complete hierarchical tree, if you want k clusters you just have to cut the k-1 longest links.

Single-Linkage Clustering: The Algorithm
Let’s now take a deeper look at how Johnson’s algorithm works in the case of single-linkage clustering.
The algorithm is an agglomerative scheme that erases rows and columns in the proximity matrix as old clusters are merged into new ones.

The N*N proximity matrix is D = [d(i,j)]. The clusterings are assigned sequence numbers 0,1,......, (n-1) and L(k) is the level of the kth clustering. A cluster with sequence number m is denoted (m) and the proximity between clusters (r) and (s) is denoted d [(r),(s)].

The algorithm is composed of the following steps:

An Example
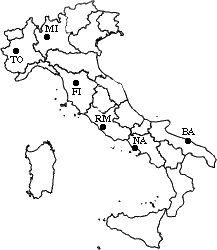
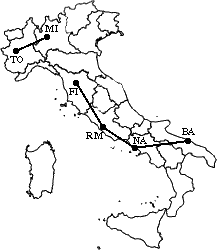
Let’s now see a simple example: a hierarchical clustering of distances in kilometers between some Italian cities. The method used is single-linkage.

Input distance matrix (L = 0 for all the clusters):

The nearest pair of cities is MI and TO, at distance 138. These are merged into a single cluster called "MI/TO". The level of the new cluster is L(MI/TO) = 138 and the new sequence number is m = 1.
Then we compute the distance from this new compound object to all other objects. In single link clustering the rule is that the distance from the compound object to another object is equal to the shortest distance from any member of the cluster to the outside object. So the distance from "MI/TO" to RM is chosen to be 564, which is the distance from MI to RM, and so on.

After merging MI with TO we obtain the following matrix:

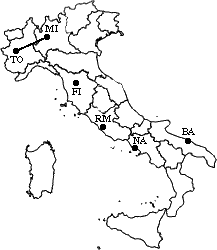
min d(i,j) = d(NA,RM) = 219 => merge NA and RM into a new cluster called NA/RM
L(NA/RM) = 219
m = 2

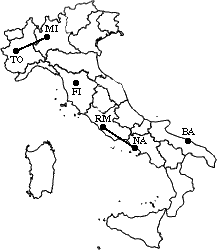
min d(i,j) = d(BA,NA/RM) = 255 => merge BA and NA/RM into a new cluster called BA/NA/RM
L(BA/NA/RM) = 255
m = 3

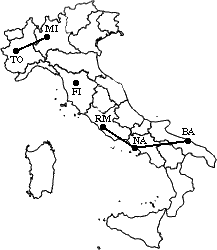
min d(i,j) = d(BA/NA/RM,FI) = 268 => merge BA/NA/RM and FI into a new cluster called BA/FI/NA/RM
L(BA/FI/NA/RM) = 268
m = 4

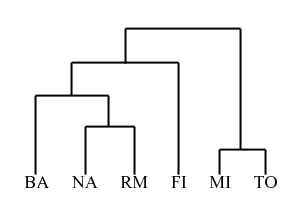
Finally, we merge the last two clusters at level 295.

The process is summarized by the following hierarchical tree:

Problems
The main weaknesses of agglomerative clustering methods are:

• they do not scale well: time complexity of at least O(n²), where n is the number of total objects;
• they can never undo what was done previously.

Bibliography

Hierarchical clustering interactive demo

Previous page | Next page