A Tutorial on Clustering Algorithms

Introduction | K-means | Fuzzy C-means | Hierarchical | Mixture of Gaussians | Links

K-Means Clustering

The Algorithm
K-means (MacQueen, 1967) is one of the simplest unsupervised learning algorithms that solve the well known clustering problem. The procedure follows a simple and easy way to classify a given data set through a certain number of clusters (assume k clusters) fixed a priori. The main idea is to define k centroids, one for each cluster. These centroids shoud be placed in a cunning way because of different location causes different result. So, the better choice is to place them as much as possible far away from each other. The next step is to take each point belonging to a given data set and associate it to the nearest centroid. When no point is pending, the first step is completed and an early groupage is done. At this point we need to re-calculate k new centroids as barycenters of the clusters resulting from the previous step. After we have these k new centroids, a new binding has to be done between the same data set points and the nearest new centroid. A loop has been generated. As a result of this loop we may notice that the k centroids change their location step by step until no more changes are done. In other words centroids do not move any more.
Finally, this algorithm aims at minimizing an objective function, in this case a squared error function. The objective function

,

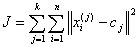where 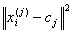is a chosen distance measure between a data point 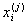and the cluster centre 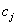, is an indicator of the distance of the n data points from their respective cluster centres.

The algorithm is composed of the following steps:

Although it can be proved that the procedure will always terminate, the k-means algorithm does not necessarily find the most optimal configuration, corresponding to the global objective function minimum. The algorithm is also significantly sensitive to the initial randomly selected cluster centres. The k-means algorithm can be run multiple times to reduce this effect.

K-means is a simple algorithm that has been adapted to many problem domains. As we are going to see, it is a good candidate for extension to work with fuzzy feature vectors.

An example
Suppose that we have n sample feature vectors x₁, x₂, ..., x_n all from the same class, and we know that they fall into k compact clusters, k < n. Let m_i be the mean of the vectors in cluster i. If the clusters are well separated, we can use a minimum-distance classifier to separate them. That is, we can say that x is in cluster i if || x - m_i || is the minimum of all the k distances. This suggests the following procedure for finding the k means:

• Make initial guesses for the means m₁, m₂, ..., m_k
• Until there are no changes in any mean
  • Use the estimated means to classify the samples into clusters
  • For i from 1 to k
    • Replace m_i with the mean of all of the samples for cluster i
  • end_for
• end_until

Here is an example showing how the means m₁ and m₂ move into the centers of two clusters.

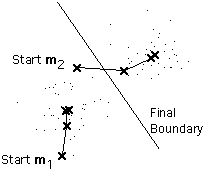
Remarks
This is a simple version of the k-means procedure. It can be viewed as a greedy algorithm for partitioning the n samples into k clusters so as to minimize the sum of the squared distances to the cluster centers. It does have some weaknesses:

• The way to initialize the means was not specified. One popular way to start is to randomly choose k of the samples.
• The results produced depend on the initial values for the means, and it frequently happens that suboptimal partitions are found. The standard solution is to try a number of different starting points.
• It can happen that the set of samples closest to m_i is empty, so that m_i cannot be updated. This is an annoyance that must be handled in an implementation, but that we shall ignore.
• The results depend on the metric used to measure || x - m_i ||. A popular solution is to normalize each variable by its standard deviation, though this is not always desirable.
• The results depend on the value of k.

This last problem is particularly troublesome, since we often have no way of knowing how many clusters exist. In the example shown above, the same algorithm applied to the same data produces the following 3-means clustering. Is it better or worse than the 2-means clustering?

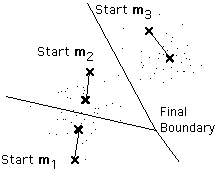
Unfortunately there is no general theoretical solution to find the optimal number of clusters for any given data set. A simple approach is to compare the results of multiple runs with different k classes and choose the best one according to a given criterion (for instance the Schwarz Criterion - see Moore's slides), but we need to be careful because increasing k results in smaller error function values by definition, but also an increasing risk of overfitting.

Bibliography

K-means interactive demo

Previous page | Next page