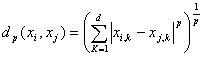Clustering - Introduction

A Tutorial on Clustering Algorithms

Clustering: An Introduction

What is Clustering?
Clustering can be considered the most important unsupervised learning problem; so, as every other problem of this kind, it deals with finding a structure in a collection of unlabeled data.
A loose definition of clustering could be “the process of organizing objects into groups whose members are similar in some way”.
A cluster is therefore a collection of objects which are “similar” between them and are “dissimilar” to the objects belonging to other clusters.
We can show this with a simple graphical example:

In this case we easily identify the 4 clusters into which the data can be divided; the similarity criterion is distance: two or more objects belong to the same cluster if they are “close” according to a given distance (in this case geometrical distance). This is called distance-based clustering.
Another kind of clustering is conceptual clustering: two or more objects belong to the same cluster if this one defines a concept common to all that objects. In other words, objects are grouped according to their fit to descriptive concepts, not according to simple similarity measures.

The Goals of Clustering
So, the goal of clustering is to determine the intrinsic grouping in a set of unlabeled data. But how to decide what constitutes a good clustering? It can be shown that there is no absolute “best” criterion which would be independent of the final aim of the clustering. Consequently, it is the user which must supply this criterion, in such a way that the result of the clustering will suit their needs.
For instance, we could be interested in finding representatives for homogeneous groups (data reduction), in finding “natural clusters” and describe their unknown properties (“natural” data types), in finding useful and suitable groupings (“useful” data classes) or in finding unusual data objects (outlier detection).

Possible Applications
Clustering algorithms can be applied in many fields, for instance:

In the first case data are grouped in an exclusive way, so that if a certain datum belongs to a definite cluster then it could not be included in another cluster. A simple example of that is shown in the figure below, where the separation of points is achieved by a straight line on a bi-dimensional plane.
On the contrary the second type, the overlapping clustering, uses fuzzy sets to cluster data, so that each point may belong to two or more clusters with different degrees of membership. In this case, data will be associated to an appropriate membership value.

Instead, a hierarchical clustering algorithm is based on the union between the two nearest clusters. The beginning condition is realized by setting every datum as a cluster. After a few iterations it reaches the final clusters wanted.
Finally, the last kind of clustering use a completely probabilistic approach.

In this tutorial we propose four of the most used clustering algorithms:

Each of these algorithms belongs to one of the clustering types listed above. So that, K-means is an exclusive clustering algorithm, Fuzzy C-means is an overlapping clustering algorithm, Hierarchical clustering is obvious and lastly Mixture of Gaussian is a probabilistic clustering algorithm. We will discuss about each clustering method in the following paragraphs.

Distance Measure
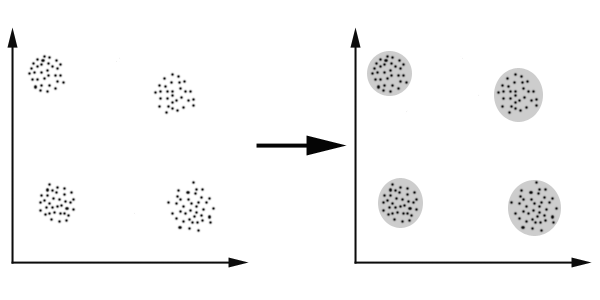
An important component of a clustering algorithm is the distance measure between data points. If the components of the data instance vectors are all in the same physical units then it is possible that the simple Euclidean distance metric is sufficient to successfully group similar data instances. However, even in this case the Euclidean distance can sometimes be misleading. Figure shown below illustrates this with an example of the width and height measurements of an object. Despite both measurements being taken in the same physical units, an informed decision has to be made as to the relative scaling. As the figure shows, different scalings can lead to different clusterings.

Notice however that this is not only a graphic issue: the problem arises from the mathematical formula used to combine the distances between the single components of the data feature vectors into a unique distance measure that can be used for clustering purposes: different formulas leads to different clusterings.
Again, domain knowledge must be used to guide the formulation of a suitable distance measure for each particular application.

Minkowski Metric
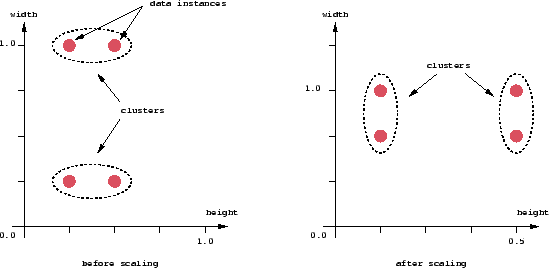
For higher dimensional data, a popular measure is the Minkowski metric,

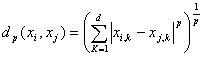
where d is the dimensionality of the data. The Euclidean distance is a special case where p=2, while Manhattan metric has p=1. However, there are no general theoretical guidelines for selecting a measure for any given application.

It is often the case that the components of the data feature vectors are not immediately comparable. It can be that the components are not continuous variables, like length, but nominal categories, such as the days of the week. In these cases again, domain knowledge must be used to formulate an appropriate measure.